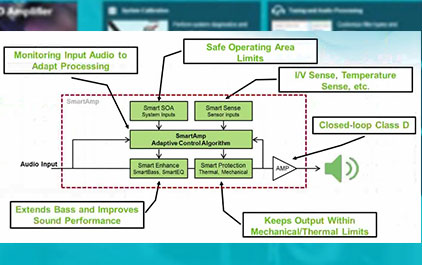
通用运算放大器
最新课程
- 电源培训授证项目-在线答疑Q&A 直播回放
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (下)
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (上)
- C2000™ Σ-Δ 滤波器调制器 (SDFM)
- C2000™ 的传感和处理功能
- C2000™ 可配置逻辑块 (CLB)
- C2000™ 模数转换器 (ADC) 培训
- C2000™ 增强型脉宽调制器 (ePWM)
- Code Composer Studio™ 快速提示
- 用于优化电源性能的 PCB 布局指南
热门课程
8.2 TI 高精度实验室 - 噪声 2
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本节视频将介绍
运放固有噪声课程的第二部分
我们将会深入运放噪声的不同区域
进一步探讨
如何将噪声频谱密度转换成 RMS 噪声
噪声的分析需要考虑运放的电压噪声源
电流噪声源和电阻噪声源
运放的增益和带宽限制
也会影响总噪声的计算结果
在接下来的视频中
我们会学习如何考虑所有的相关参数
从而得到总的峰峰值输出噪声
在进行噪声计算前
我们需要知道一个很关键的概念
即 noise gain 噪声增益
噪声增益是指
运放电路对于总的输入端噪声的增益
输入端噪声源模型被放置在
运放的同相输入端
噪声增益在某些情况下并不等于信号增益
这里给出的例子中 噪声增益是 2
而信号增益则是 -1
换句话说相对于信号源来说
这个电路是反相输入的配置
而相对于噪声电压源来说
这是一个同相输入运放
这里总结了如何将电压频谱密度
转换成为 RMS 噪声电压
再进一步转换成
为峰峰值的一般过程
将电压频谱密度转换成 RMS
需要先将频谱密度函数平方
再对其在想要的带宽范围内进行积分
积分之后开根号即可得到 RMS 值
这样的一个过程
其实是对功率频谱密度进行积分
然后再开根号转换成电压或者电流的过程
大家可以回忆一下功率的表达式
P = V2 / R 和 P = I2 x R
对于这一点我们接下来会深入探讨
得到 RMS 噪声电压之后
将其乘以 6 就可以得到峰峰值了
我们在之前视频中提到
这里的系数 6
只是一个统计意义上的估计系数
它代表的是 +/-3 个标准差
或者 6 个 σ
其意味着还有 0.3% 的概率
噪声的峰峰值会在这个范围之外
这里我们简单回顾一下积分的方式
积分其实就是求曲线以下
所包围的区域的面积
这里所示的是一个长方形区域
所以其积分就是简单地宽乘以高
这个简单的原理
会对我们之后做噪声维度分析很有帮助
在这一页中
我们会重申将电压频谱密度
转换成 RMS 电压的方法
在噪声分析中
一个常见的误解是
对电压或者电流频谱密度
进行直接积分就可以得到总噪声
但事实上正确的做法
是对功率频谱密度进行积分
上面所示的这个例子
就是对电压频谱密度
直接进行积分的结果
回顾一下之前我们讲过
对长方形的积分是宽乘以高
所以使用这个原理
这里就是 5V/√Hz x 10Hz
注意到最后我们得到的单位很奇怪
是 V*Hz /√Hz
但正确的单位应该是 V(伏特)
根据维度分析
或者说计算结果的单位我们可以得知
直接对电压频谱密度进行积分
是无法正确地将频谱密度转换成 RMS 的
下面所示的例子
则是对功率频谱密度进行积分
回忆一下功率的表达式
用电压计算是 V2/R
用电流计算是 I2*R
对功率频谱密度进行积分再开根号
就可以得到单位为伏特的结果
因此计算总噪声的时候
要记住对功率频谱积分
频谱密度曲线有两个区域
1/f 区域和宽带区域
此前我们曾在时域里探讨过这两个区域
1/f 噪声发生在低频区域
对于其电压和电流频谱密度来说
其斜率都是根号频率分之一
即 1/√f
由于功率频谱密度是电压频谱密度的平方
所以功率频谱密度的斜率即为 1/f
这也是我们把这个区域
叫做 1/f 区域的原因
宽带噪声或者白噪声
则有一个平坦的频谱密度
接下来我们深入学习一下这个 1/f 噪声
为了计算 1/f 区域相关的 RMS 噪声
我们需要对其功率频谱密度积分再开根号
右手边给出了这个计算方程
之后我们会详细介绍这些方程
并在实际的例子中进行练习
现在我们来看看宽带区域
注意到在宽带区域的末尾
加了一个低通滤波器
原因是所有实际的电路都有某些带宽限制
如果没有带宽限制
积分出来的总噪声会是无限大的一个值
同时这里我们也可以注意到宽带区域
是一直延伸到低频范围的
事实上 如果同时考虑两个区域
你可以看见 1/f 区域和宽带区域
都出现在低频和高频范围
在低频的范围中
1/f 噪声是主导的
而宽带噪声也出现在这个范围内
在高一些的频率范围里
宽带噪声是主导的
但是 1/f 也会出现在这些频率中
但是 1/f 也会出现在这些频率中
计算总噪声
需要将这两个区域的
噪声平方求和再开根号
接下来我们将探讨噪声带宽
正如之前提到
由于电路自带的带宽限制
现实生活中
系统的噪声带宽都有一个低通滤波响应
上面图中绿色部分显示的就是低通响应
我们将其等效为一个长方形的低通滤波器
并加到频带响应即蓝色区域
这个长方形的过滤器
我们称其为 brick wall filter
矩形滤波器
其面积和上图绿色区域所代表的
低通滤波器是相等的
它能使所有低于截止频率的信号无损通过
同时所有高于截止频率的信号
则被无限的衰减
从而在幅频特性曲线上呈现矩形
因此而得名 矩形滤波器
通过这样的一个等效
我们可以很容易地进行积分
注意到右边计算噪声带宽的式子中包含积分
一般来说
这个式子只需要使用一次
根据它我们来计算不同阶数的过滤器
所对应的修正系数
在这个例子中
通过使用这个式子
计算得到 1 阶过滤器
所对应的修正系数是 1.57
下一页里我们就会看到其它阶数的过滤器
所对应的修正系数
右边的表格给出了矩形过滤器的修正系数
根据这些系数我们计算噪声带宽
将 -3dB 带宽乘以修正系数 Kn
便可以得到噪声带宽
注意到 随着极点个数的增加
修正系数越来越接近 1
原因就在于
高阶滤波器曲线下降的速度更快
从而呈现更陡的趋势
同时还要考虑的是
增益峰值也会影响噪声带宽
增益峰值也会影响噪声带宽
所以实际电路中
真实的噪声带宽还会不一样
我们已经知道噪声带宽的关系式
接下来就可以进行运放噪声频谱密度
到 RMS 噪声的转换计算
这里的第一个方程
是我们刚介绍过的噪声带宽方程
使用之前给出的表格
选择合适的 Kn 值
然后将信号增益转换成噪声增益
这里的第二个方程给出了
从频谱密度到 RMS 噪声转换的过程
En_BB 是 RMS 噪声
通过将宽带噪声频谱密度
和噪声带宽的开根号值相乘得到
宽带频谱密度
可以从运放数据手册的频谱密度曲线中读到
噪声频谱密度到 RMS 噪声的转换关系
是非常重要的 最好能够记住
可以联系这个式子中的单位来帮助记忆
频谱密度单位是 nV/√Hz
乘以噪声带宽开根号即√Hz
这样一来
√Hz 这一单位就相消了
从而得到 RMS 电压的单位伏特
现在我们来看 1/f 噪声方程
第一个方程 en_normal
给出了归一化到 1Hz 的 1/f 噪声
它代表的是
在 1/f 曲线上任取一个点
将其频谱密度等效到
1Hz 时所对应的密度值
一般来说
最好选择最低频率下面的 enf
因为这样可以保证 1/f 噪声是主导的
第二个方程计算的是 1/f 区域的 RMS 总噪声
注意到这里使用的
是第一个方程计算得到的
归一化到 1Hz 的 1/f 噪声
还使用了高频截止频率和低频截止频率
在这里使用高频截止频率是不难理解的
因为它代表的是系统带宽的限制
但是为什么
我们需要一个低频截止频率限制呢
一般我们看到的噪声频谱密度
其 x 轴通常是对数形式的
如果我们将其表示成线性的 x 轴
可以清楚地看到
噪声在 0Hz 的时候是无限大的
0Hz 所对应时时间是无穷大
这在实际应用中并不可能实现
所以在实际应用中
我们考虑低频截止频率为 0.1Hz
0.1Hz 对应的观察周期是 10s
在之后的视频中
我们会进一步探讨低频噪声
及长时间观测噪声的结果
在下面一个视频中
我们会给出一个完整的噪声分析例子
这个例子使用
OPA627 于一个同相输入的配置中
输出端的总噪声是运放电压噪声
运放电流噪声和电阻噪声的总和
我们会探讨频
谱密度曲线中的 1/f 区域和宽带区域
以及电路的噪声带宽和噪声增益
以上就是本节视频的所有内容
谢谢观看
请准备好下面的一个小测试
看看你是否已掌握本次内容
-
 未学习 1.1 TI 高精度实验室 - 介绍
未学习 1.1 TI 高精度实验室 - 介绍
-
 未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
-
 未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
-
 未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
-
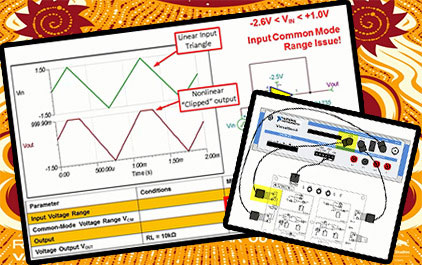 未学习 3.1 TI 高精度实验室 - 输入输出限制
未学习 3.1 TI 高精度实验室 - 输入输出限制
-
 未学习 3.2 输入和输出限制 2
未学习 3.2 输入和输出限制 2
-
 未学习 3.3 输入和输出限制 3
未学习 3.3 输入和输出限制 3
-
 未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
-
 未学习 4.1 功率与温度
未学习 4.1 功率与温度
-
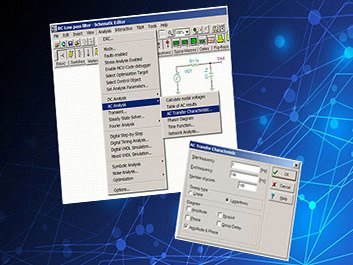 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
-
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
-
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
-
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
-
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验
-
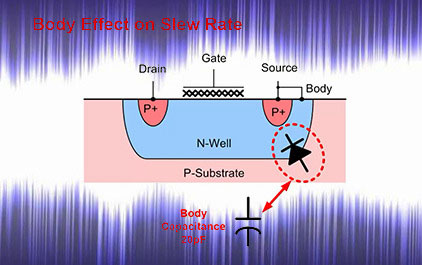 未学习 6.1 TI 高精度实验室 - 压摆率 1
未学习 6.1 TI 高精度实验室 - 压摆率 1
-
 未学习 6.2 TI 高精度实验室 - 压摆率 2
未学习 6.2 TI 高精度实验室 - 压摆率 2
-
 未学习 6.3 TI 高精度实验室 - 压摆率 3
未学习 6.3 TI 高精度实验室 - 压摆率 3
-
 未学习 6.4 TI 高精度实验室 - 压摆率 实验
未学习 6.4 TI 高精度实验室 - 压摆率 实验
-
 未学习 7.1 共模抑制
未学习 7.1 共模抑制
-
 未学习 7.2 电源抑制
未学习 7.2 电源抑制
-
 未学习 8.1 TI 高精度实验室 - 噪声 1
未学习 8.1 TI 高精度实验室 - 噪声 1
-
 未学习 8.2 TI 高精度实验室 - 噪声 2
未学习 8.2 TI 高精度实验室 - 噪声 2
-
 未学习 8.3 TI 高精度实验室 - 噪声 3
未学习 8.3 TI 高精度实验室 - 噪声 3
-
 未学习 8.4 TI 高精度实验室 - 噪声 4
未学习 8.4 TI 高精度实验室 - 噪声 4
-
 未学习 8.5 TI 高精度实验室 - 噪声 5
未学习 8.5 TI 高精度实验室 - 噪声 5
-
 未学习 8.6 TI 高精度实验室 - 噪声 6
未学习 8.6 TI 高精度实验室 - 噪声 6
-
 未学习 8.7 TI 高精度实验室 - 噪声 7
未学习 8.7 TI 高精度实验室 - 噪声 7
-
 未学习 8.8 TI 高精度实验室 - 噪声 8
未学习 8.8 TI 高精度实验室 - 噪声 8
-
 未学习 8.9 TI 高精度实验室 - 噪声 实验
未学习 8.9 TI 高精度实验室 - 噪声 实验
-
 未学习 9.1 低失真运算放大器的设计-1
未学习 9.1 低失真运算放大器的设计-1
-
 未学习 9.2 低失真运算放大器的设计-2
未学习 9.2 低失真运算放大器的设计-2
-
 未学习 9.3 低失真运算放大器的设计-3
未学习 9.3 低失真运算放大器的设计-3
-
 未学习 9.4 低失真运算放大器的设计-4
未学习 9.4 低失真运算放大器的设计-4
-
 未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
-
 未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
-
 未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
-
 未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
-
 未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
-
 未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
-
 未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
-
 未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
-
 未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
-
 未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
-
 未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
-
 未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
-
 未学习 13.1 电流反馈型运算放大器
未学习 13.1 电流反馈型运算放大器
-
 未学习 13.2 电流反馈运放
未学习 13.2 电流反馈运放
-
 未学习 14.1 如何分析合成器相位噪声
未学习 14.1 如何分析合成器相位噪声
-
 未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
-
 未学习 15.2 全差分放大器 — FDA的输入输出和共模
未学习 15.2 全差分放大器 — FDA的输入输出和共模
-
 未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
-
 未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
-
 未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
-
 未学习 (中文)3.2 输入和输出限制 2
未学习 (中文)3.2 输入和输出限制 2
-
 未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
-
 未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
-
 未学习 运算放大器失真:简介
未学习 运算放大器失真:简介
-
 未学习 (中文)反相输入电容
未学习 (中文)反相输入电容
-
 未学习 (中文)断开差分放大器上的环路
未学习 (中文)断开差分放大器上的环路
-
 未学习 (中文)带宽 - 波特图截止频率
未学习 (中文)带宽 - 波特图截止频率
-
 未学习 (中文)带宽 - 增益和 GBW
未学习 (中文)带宽 - 增益和 GBW
-
 未学习 (中文)带宽 - 同相增益和极点
未学习 (中文)带宽 - 同相增益和极点
-
 未学习 (中文)带宽 - AOL 增益转换率
未学习 (中文)带宽 - AOL 增益转换率
-
 未学习 (中文)带宽 - 实验
未学习 (中文)带宽 - 实验
-
 未学习 (中文)转换率介绍
未学习 (中文)转换率介绍
-
 未学习 (中文)稳定时间
未学习 (中文)稳定时间
-
 未学习 (中文)信号响应
未学习 (中文)信号响应
-
 未学习 (中文)运算放大器失真:简介
未学习 (中文)运算放大器失真:简介
-
 未学习 (中文)输入级
未学习 (中文)输入级
-
 未学习 (中文)光谱密度
未学习 (中文)光谱密度
-
 未学习 (中文)计算 RMS 噪声
未学习 (中文)计算 RMS 噪声
-
 未学习 (中文)计算总噪声
未学习 (中文)计算总噪声
-
 未学习 (中文)简化计算
未学习 (中文)简化计算
-
 未学习 (中文)噪声spice模拟
未学习 (中文)噪声spice模拟
-
 未学习 (中文)验证噪声模型
未学习 (中文)验证噪声模型
-
 未学习 (中文)测量系统噪声
未学习 (中文)测量系统噪声
-
 未学习 (中文)1/F 噪声
未学习 (中文)1/F 噪声
-
 未学习 (中文)噪声 - 实验
未学习 (中文)噪声 - 实验
-
 未学习 理想的无源元件
未学习 理想的无源元件