通用运算放大器
最新课程
- 电源培训授证项目-在线答疑Q&A 直播回放
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (下)
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (上)
- C2000™ Σ-Δ 滤波器调制器 (SDFM)
- C2000™ 的传感和处理功能
- C2000™ 可配置逻辑块 (CLB)
- C2000™ 模数转换器 (ADC) 培训
- C2000™ 增强型脉宽调制器 (ePWM)
- Code Composer Studio™ 快速提示
- 用于优化电源性能的 PCB 布局指南
热门课程
5.2 TI 高精度实验室 - 带宽 2
大家好
欢迎来到 TI Precision Labs
德州仪器高精度实验室
本次视频将介绍
运算放大器的 Bandwidth 带宽的第二部分
我们将探讨 open loop gain
开环回路增益
closed loop gain 闭环回路增益
gain bandwidth product 增益带宽积
Quiescent Current 静态电流与带宽的关系
也将仿真电路的带宽
并验证我们的计算结果
运算放大器的开环回路增益
或 Aol 代表由运算放大器
施加到输入端电压差的增益
运算放大器的 Aol 是无限大
然而真实世界的运算放大器
有超过 100 万 V/V
或 120dB 的开环回路增益
为了使一个放大器稳定
Negative feedback 负回授是必要的
可以经由 Rf 和 R1 来实现
有时被称为闭合回路
Rf 和 R1 代表 β 的网络 或回授系数
β 是经由测量 Vout 回授到运算放大器的
反相输入端变化来求得
在这个电路中我们看到 Rf 和 R1
产生一个电压分压器
因此 β=R1/(R1+Rf)
除运算放大器的开环回路增益
我们有所谓的闭环回路增益或 Acl
该方程 Acl=Aol/(1+Aolβ)
其中的 Aolβ 被称为回路增益
如图所示 这个方程式可以重新整理
闭环回路这一方程式可以简化
是由于有非常大的回路增益或 Aolβ
纵观回路增益公式可以看出
当 Aolβ 增加到无限大
你可以忽略分母中的 1
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得到 1/β
代入 β 可以得到 1+Rf/R1 的
闭环回路增益
这是一个常见的 none inverting
同相放大器闭环回路增益公式
重点是这个公式
只适用于开环回路增益非常高时
稍后我们将看到
当开环回路增益低会发生什么事情
然而在现实世界中
运算放大器的开环回路增益
具有低频的 dominant pole 主极点
如图所示 可以被看做是一个 RC filter滤波器
此仿真描绘了真实世界
运算放大器开环回路增益
在直流或低频 Aol 是非常大的
在这种情况下
它是 120dB 或 100万V/V
随着频率的增加 Aol 以 -20dB/dec 的速率降低
我们看到在 10MHz 时
开环回路增益为 0dB 或 1V/V
现在我们明白开环回路增益
会随着频率降低
此现象如何影响我们的闭环回路增益呢
回想一下 Aolβ 被称为回路增益
如果我们绘制了开环回路增益和 1/β 在对数轴
回路增益为两条曲线之间的差值
数学证明回路增益是 Aol 减掉 1/β
如底下的方程式所示
在这个例子中
1/β 为水平虚线在 20dB
注意 闭环回路增益在低频时为 1/β
在高频时为 Aol 曲线
还要注意在这 1/β 曲线和 Aol 曲线交错的点
是闭环回路带宽
让我们更深入地看看为什么闭环回路增益
在低频时为 1/β
而在高频时为 Aol
在低频时回路增益或 Aolβ 很大
请注意闭环回路增益为
Aol/(1+Aolβ)
所以对于较大 Aolβ
可以忽略 1 这一项
公式可简化为 Aol/Aolβ
将分子分母的 Aol 相消可得 1/β
在这种情况下
1/β 是一个熟悉的同相放大器增益方程式
1/β 是一个熟悉的同相放大器增益方程式
值为1+Rf/R1
在高频时 Aolβ 很小
请注意 闭环回路增益为 Aol/(1+Aolβ)
所以对于小的 Aolβ 值
就可以忽略 Aolβ
这样一来就只剩下 Aol/1
或者说就是 Aol
因此当 Aolβ 变小
闭环回路增益跟随 Aol 曲线
我们定义的电路的带宽为 1/β
和 Aol 曲线相交的频率
因此运算放大器数据表中
Aol 曲线可以近似到电路所需的闭环回路增益带宽
然而请注意 X 轴是对数的
因此以图形方式选定的带宽可能不够精确
另一种方法来确定带宽
是使用运算放大器数据表中的增益带宽积产品规格
增益带宽积是线性增益和带宽的乘积
因此在给定两个变数中的一个
可以得到另外一个解
例如让我们计算 OPA827 在 100V/V 的带宽吧
从数据表我们可以得知
增益带宽积为 22MHz
为求解带宽 从增益带宽公式告诉我们
带宽为增益带宽积除以线性增益
将 OPA827 增益带宽积 22MHz/100V/V 的增益
可以得到 220kHz 带宽
此计算可由观察数据表中 OPA827
开环回路增益来验证
如果画一条水平线在 100V/V
或 40dB 的闭环回路增益
直到它相交 Aol 我们找到了相应的带宽
大约为 200kHz
可以注意到 通过计算我们发现
带宽为 220kHz
它解决了图解可能错误地解释带宽为 200kHz
请注意计算出的带宽
须当 Aol 局限于
-20dB/dec 的速率下降才是有效的
虽然大部分的运算放大器都符合
但也有些特定的增益带宽积是有限的范围
此外考虑到数据表有增益带宽积
和 Aol 曲线的典型值
通常可以预期该值在室温下的变异数高达± 30%
在规定的温度范围外
可能有附加正负 30% 误差的变化
因此当考虑到放大器的带宽时
建议设计时保留您的设计裕度
现在让我们与 TINA-TI 仿真做比较
这里我们将一个 OPA140 设计为同相放大器组态
100V/V 或是 40dB 的闭环回路增益
该 OPA140 具有 11MHz 的增益带宽积
代入我们的闭环回路增益 100V/V
可以求出带宽为110kHz
在这里我们仿真的电路的闭环回路带宽
在 -3dB 点或 37dB 仿真带宽为 118kHz
虽然不完全一样
但我们计算和仿真结果是正相关的
最后让我们来看一下
一系列 TI 运算放大器的增益带宽
和其相对应的静态电流 Iq
此页我们列出增益带宽范围
从 12kHz 到 600MHz 放大器
OPA369 是一个非常低带宽的放大器
该电路是特别设计为非常低的静态电流
仅有 0.8uA 称为微功率电路
1MHz 为普遍放大器的带宽范围
如 OPA277
而 OPA350 和 OPA211 则具有更宽的带宽
以方便驱动 A/D 转换器
和其他高带宽应用
对非常高速应用中
可使用如 OPA835 和 OPA847
在一般情况下较宽的带宽运算放大器
需要较多的静态电流
不过有例外如 OPA835
那么为什么带宽和静态电流有关联
让我们来看看双极性和 CMOS 晶体管的物理关系
请注意 这里不是要深入理解晶体管理论
来了解放大器的带宽
这里的关键是
表示放大器带宽和静态电流间的物理原理
观察双极晶体管和 MOSFET 的 Transductions
转导或电流增益
可以看出 collector 基极和 drain 漏极
电流的直接关系
转导取倒数可得阻抗或 rgm
rgm 是运算放大器内部第一级的动态输出阻抗
此输出阻抗驱动米勒电容 Cc
rgm 和 Cc 的串联组合形成一个低通滤波器
该低通滤波器的主极点产生放大器内部的带宽
事实上你可以看到第三个方程式
是 RC 带宽公式
BW=2πRC 在最后的方程式
我们代入原有的 gm 公式来说明 gm 带宽的关联
其显示增加电流消耗
直接增加双极性运算放大器的带宽
但是如果是 MOSFET
带宽将依漏极电流平方根的比例增加
所以相较于双极晶体管
MOSFET 需要增加更大的电流来增加带宽
总结 这个视频讨论开环回路和闭环回路增益
增益带宽积 静态电流与带宽
我们还仿真电路的带宽
并显示带宽与我们计算结果的关联性
感谢您的时间
请尝试测验来检视对这个视频内容的理解吧
-
 未学习 1.1 TI 高精度实验室 - 介绍
未学习 1.1 TI 高精度实验室 - 介绍
-
 未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
未学习 1.2 TI 高精度实验室 - 国家仪器虚拟测试仪概述
-
 未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
未学习 2.1 TI 高精度实验室 - 输入失调电压与输入偏置电流
-
 未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
未学习 2.2 TI 高精度实验室 - 输入失调电压与输入偏置电流 实验
-
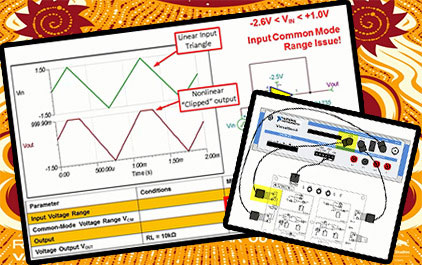 未学习 3.1 TI 高精度实验室 - 输入输出限制
未学习 3.1 TI 高精度实验室 - 输入输出限制
-
 未学习 3.2 输入和输出限制 2
未学习 3.2 输入和输出限制 2
-
 未学习 3.3 输入和输出限制 3
未学习 3.3 输入和输出限制 3
-
 未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
未学习 3.4 TI 高精度实验室 - 输入输出限制 实验
-
 未学习 4.1 功率与温度
未学习 4.1 功率与温度
-
 未学习 5.1 TI 高精度实验室 - 带宽 1
未学习 5.1 TI 高精度实验室 - 带宽 1
-
 未学习 5.2 TI 高精度实验室 - 带宽 2
未学习 5.2 TI 高精度实验室 - 带宽 2
-
 未学习 5.3 TI 高精度实验室 - 带宽 3
未学习 5.3 TI 高精度实验室 - 带宽 3
-
 未学习 5.4 TI 高精度实验室 - 带宽 4
未学习 5.4 TI 高精度实验室 - 带宽 4
-
 未学习 5.5 TI 高精度实验室 - 带宽 实验
未学习 5.5 TI 高精度实验室 - 带宽 实验
-
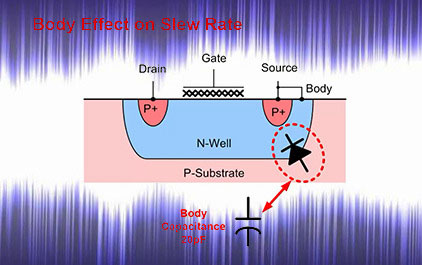 未学习 6.1 TI 高精度实验室 - 压摆率 1
未学习 6.1 TI 高精度实验室 - 压摆率 1
-
 未学习 6.2 TI 高精度实验室 - 压摆率 2
未学习 6.2 TI 高精度实验室 - 压摆率 2
-
 未学习 6.3 TI 高精度实验室 - 压摆率 3
未学习 6.3 TI 高精度实验室 - 压摆率 3
-
 未学习 6.4 TI 高精度实验室 - 压摆率 实验
未学习 6.4 TI 高精度实验室 - 压摆率 实验
-
 未学习 7.1 共模抑制
未学习 7.1 共模抑制
-
 未学习 7.2 电源抑制
未学习 7.2 电源抑制
-
 未学习 8.1 TI 高精度实验室 - 噪声 1
未学习 8.1 TI 高精度实验室 - 噪声 1
-
 未学习 8.2 TI 高精度实验室 - 噪声 2
未学习 8.2 TI 高精度实验室 - 噪声 2
-
 未学习 8.3 TI 高精度实验室 - 噪声 3
未学习 8.3 TI 高精度实验室 - 噪声 3
-
 未学习 8.4 TI 高精度实验室 - 噪声 4
未学习 8.4 TI 高精度实验室 - 噪声 4
-
 未学习 8.5 TI 高精度实验室 - 噪声 5
未学习 8.5 TI 高精度实验室 - 噪声 5
-
 未学习 8.6 TI 高精度实验室 - 噪声 6
未学习 8.6 TI 高精度实验室 - 噪声 6
-
 未学习 8.7 TI 高精度实验室 - 噪声 7
未学习 8.7 TI 高精度实验室 - 噪声 7
-
 未学习 8.8 TI 高精度实验室 - 噪声 8
未学习 8.8 TI 高精度实验室 - 噪声 8
-
 未学习 8.9 TI 高精度实验室 - 噪声 实验
未学习 8.9 TI 高精度实验室 - 噪声 实验
-
 未学习 9.1 低失真运算放大器的设计-1
未学习 9.1 低失真运算放大器的设计-1
-
 未学习 9.2 低失真运算放大器的设计-2
未学习 9.2 低失真运算放大器的设计-2
-
 未学习 9.3 低失真运算放大器的设计-3
未学习 9.3 低失真运算放大器的设计-3
-
 未学习 9.4 低失真运算放大器的设计-4
未学习 9.4 低失真运算放大器的设计-4
-
 未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
未学习 10.1 TI 高精度实验室 - 运算放大器:稳定性分析 1
-
 未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
未学习 10.2 TI 高精度实验室 - 运算放大器:稳定性分析 2
-
 未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
未学习 10.3 TI 高精度实验室 - 运算放大器:稳定性分析 3
-
 未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
未学习 10.4 TI 高精度实验室 - 运算放大器:稳定性分析 4
-
 未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
未学习 10.5 TI 高精度实验室 - 运算放大器:稳定性分析 5
-
 未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
未学习 10.6 TI 高精度实验室 - 运算放大器:稳定性分析 6
-
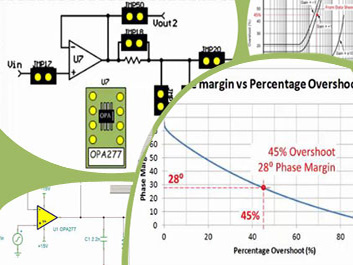 未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
未学习 10.7 TI 高精度实验室 - 运算放大器:稳定性 - 实验
-
 未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
未学习 11.1 TI 高精度实验室 - 静电释放 (ESD)
-
 未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
未学习 12.1 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 1
-
 未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
未学习 12.2 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 2
-
 未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
未学习 12.3 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 3
-
 未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
未学习 12.4 TI 高精度实验室 - 运算放大器:电气过应力 (EOS) 4
-
 未学习 13.1 电流反馈型运算放大器
未学习 13.1 电流反馈型运算放大器
-
 未学习 13.2 电流反馈运放
未学习 13.2 电流反馈运放
-
 未学习 14.1 如何分析合成器相位噪声
未学习 14.1 如何分析合成器相位噪声
-
 未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
未学习 15.1 全差分放大器 — 差分信号和FDA的介绍
-
 未学习 15.2 全差分放大器 — FDA的输入输出和共模
未学习 15.2 全差分放大器 — FDA的输入输出和共模
-
 未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
未学习 15.3 全差分放大器 — FDA的稳定性和相位裕量
-
 未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
未学习 15.4 全差分放大器 — FDA的噪声和噪声控制
-
 未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
未学习 15.5 全差分放大器 — 设计用于驱动差分输入ADC的前端电路
-
 未学习 (中文)3.2 输入和输出限制 2
未学习 (中文)3.2 输入和输出限制 2
-
 未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
未学习 (中文)14.3 电流反馈型运算放大器 Spice 仿真
-
 未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
未学习 (中文)15.5 设计用于驱动差分输入ADC的前端电路
-
 未学习 运算放大器失真:简介
未学习 运算放大器失真:简介
-
 未学习 (中文)反相输入电容
未学习 (中文)反相输入电容
-
 未学习 (中文)断开差分放大器上的环路
未学习 (中文)断开差分放大器上的环路
-
 未学习 (中文)带宽 - 波特图截止频率
未学习 (中文)带宽 - 波特图截止频率
-
 未学习 (中文)带宽 - 增益和 GBW
未学习 (中文)带宽 - 增益和 GBW
-
 未学习 (中文)带宽 - 同相增益和极点
未学习 (中文)带宽 - 同相增益和极点
-
 未学习 (中文)带宽 - AOL 增益转换率
未学习 (中文)带宽 - AOL 增益转换率
-
 未学习 (中文)带宽 - 实验
未学习 (中文)带宽 - 实验
-
 未学习 (中文)转换率介绍
未学习 (中文)转换率介绍
-
 未学习 (中文)稳定时间
未学习 (中文)稳定时间
-
 未学习 (中文)信号响应
未学习 (中文)信号响应
-
 未学习 (中文)运算放大器失真:简介
未学习 (中文)运算放大器失真:简介
-
 未学习 (中文)输入级
未学习 (中文)输入级
-
 未学习 (中文)光谱密度
未学习 (中文)光谱密度
-
 未学习 (中文)计算 RMS 噪声
未学习 (中文)计算 RMS 噪声
-
 未学习 (中文)计算总噪声
未学习 (中文)计算总噪声
-
 未学习 (中文)简化计算
未学习 (中文)简化计算
-
 未学习 (中文)噪声spice模拟
未学习 (中文)噪声spice模拟
-
 未学习 (中文)验证噪声模型
未学习 (中文)验证噪声模型
-
 未学习 (中文)测量系统噪声
未学习 (中文)测量系统噪声
-
 未学习 (中文)1/F 噪声
未学习 (中文)1/F 噪声
-
 未学习 (中文)噪声 - 实验
未学习 (中文)噪声 - 实验
-
 未学习 理想的无源元件
未学习 理想的无源元件