温度传感器和控制 IC
最新课程
- 电源培训授证项目-在线答疑Q&A 直播回放
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (下)
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (上)
- C2000™ Σ-Δ 滤波器调制器 (SDFM)
- C2000™ 的传感和处理功能
- C2000™ 可配置逻辑块 (CLB)
- C2000™ 模数转换器 (ADC) 培训
- C2000™ 增强型脉宽调制器 (ePWM)
- Code Composer Studio™ 快速提示
- 用于优化电源性能的 PCB 布局指南
热门课程
3.1 TI 高精度实验室 - 温度传感器:校准与补偿
大家好,欢迎观看 TI 高精度实验室
视频,本视频将讨论如何 使用温度传感器进行
校准和补偿。
在本视频中,我们 将讨论使用温度
传感器校准 和补偿系统的
概念。
通常,补偿意味着 迁移一个或多个
可变参数对 系统行为的
影响。
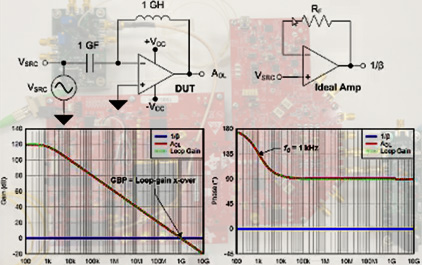
让我们以一个 小信号反相
放大器为例。
理想电路的增益 表示为反馈电阻器
除以输入电阻器。
不过,在实际的实现过程中, 情况可能并非如此,
因为使用的电阻器与
温度相关。
这称为电阻的 温度系数,
或 TCR,以 百万分率/摄氏度为单位。
制造商在 数据表中
提供组件 关于 25 摄氏度
室温的 TCR 最大限值。
在该示例中,让我们 进一步假设反馈
电阻器 Rf 的 值为 2 千欧。
输入电阻器 Rn 的 值为 1 千欧。
两个电阻器 都具有正负
100 ppm/摄氏度的 TCR, 在 25 摄氏度下指定。
这会导致理想 反相增益 2。
针对 125 摄氏度 求解 TCR 公式,
可得到 Rf 的 变化量为
正负 20 欧姆, Rn 的变化量
为正负 10 欧姆。
正如前面所计算,
该电路的理想增益幅度是 2。
让我们假设输入小信号
是锯齿波,该波以 增益 2 进行放大。
Vout 的虚线显示了 可能的最大输出
信号电平。
在该理想情况下, 输出信号等于
最大输出电平。
现在,在 125 摄氏度下, 如果两个电阻器
使最大正负 TCR 产生漂移,
那么增益保持不变。
输入信号也保持不变。
不过,如果漂移不相同,
那么结果就会截然不同。
如果 Rf 具有正漂移, Rn 具有负漂移,那么
该电路的增益 从 2 变为 2.04。
这会导致输出信号 超出最大信号电平,
从而产生削波 并在输出中引入
谐波失真。
如果 Rf 具有负漂移, Rn 具有正漂移,那么
该电路的增益 从 2 变为 1.96。
这会导致输出 信号放大率
随温度的 升高而减小。
我们先前已看到 温度如何影响
简单反相放大器的 行为,因此我们知道
对于不断变化的 温度,需要应用
某种形式的迁移或 补偿,这一点至关重要。
一种简单的补偿 方法是将一个
可变电阻器 与输入和
反馈电阻器 进行串联。
不过,要确定 实现的补偿量,
我们必须知道 我们计划对其
进行补偿的 组件周围的
系统温度。
在这种情况下需要 使用温度传感器元件。
一旦我们可以 准确地确定该温度,
就可以对电路应用 正确的补偿,从而
确保无论温度 如何变化,都使用
相同的增益对 输出进行放大。
我们已经了解 温度补偿,那么
现在我们将介绍 什么是温度校准
以及如何利用温度校准 为给定的电路
执行补偿。
如前所述,由于环境
温度变化或自热效应,
所有组件都会 引入某种程度的
温度误差。
对于该示例,我们 将再次采用反相
放大器电路。
x 轴表示温度。
y 轴表示增益。
绿线表示理想 增益 2,我们
希望电路在整个工作
温度范围内具有该增益。
理想增益周围的 红框表示由于
组件值的变化 而导致的增益
误差 --
在本例中,是由于温度而 导致的电阻器值变化。
我们的目的是通过 补偿将增益误差降低至
可接受的限值, 如绿框所示。
这是通过校准来实现的。
可以根据需要 补偿的误差类型
来使用不同类型的校准 方法,我们接下来将
对此进行介绍。
最基本的方法是单点校准,
如此处的图所示。
当在工作温度范围内误差
保持恒定时,使用单点校准
技术。
如果测量的增益 大于理想增益,
误差为正值,如果测量的 增益小于理想增益,误差
为负值。
如果电阻器具有的 容差误差和 TCR 都
以某个比例变化, 从而导致实际增益
在其工作 温度范围内
保持不变,则会 发生这种情况。
在这种情况下, 只有一个电阻器
必须调节,从而 使总增益尽可能
接近理想增益。
绿框显示了 应用误差的
可接受限值。
为了执行单点校准,
在参考温度下 测量增益误差。
然后计算所需的补偿量。
然后调节可变电阻器,从而
使总增益误差处于 应用的可接受限值
之内。
下一种校准方法是两点校准。
实际上,可能不具有两个
以确切的比例 变化的电阻器。
这会导致增益斜率, 进而导致增益随
温度的升高而增大, 或随温度的升高
而减小。
绿框显示了应用误差的
可接受限值。
为了执行两点校准,
在工作范围的最低温度下
测量系统输出。
在工作范围的最高温度下
执行相同的过程。
确定增益区域后, 可以相应地改变
一个或两个电阻器的 大小,从而使增益
误差处于可接受的 工作范围之内。
对于具有非线性响应的
系统,使用多点校准。
该方法是最复杂的方法,
因为它需要系统 设计人员了解
实际测量的响应 并以最合适的
方式将其代入可以 线性化的公式中。
例如,寄生引线 电感和迹线电容
可能改变小信号 放大器的行为,
输入信号频率和温度导致
非线性曲线。
多点校准需要 在多个温度下
及其输入信号 频率的多个点处
测量传递函数, 或者在本示例中
为增益。
然后对小信号段 进行线性化,以形成
具有更高线性度 并且能够通过
调节可变电阻器 进行温度补偿的
增益曲线。
综上所述,本视频讨论了温度
如何影响所有电路的
响应以及为何 需要补偿。
我们还讨论了 可以使用的校准
技术类型,其依据是
系统的传递函数会 如何响应温度变化。
谢谢观看。
-
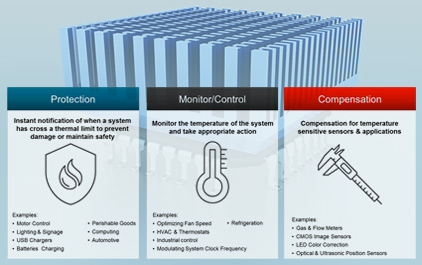 未学习 1.1 TI 高精度实验室 - 温度传感器:温度感应概述
未学习 1.1 TI 高精度实验室 - 温度传感器:温度感应概述
-
 未学习 1.2 TI 高精度实验室 - 温度传感器:温度传感器技术
未学习 1.2 TI 高精度实验室 - 温度传感器:温度传感器技术
-
 未学习 2.1 TI 高精度实验室 - 温度传感器:传感器精度误差和重复性
未学习 2.1 TI 高精度实验室 - 温度传感器:传感器精度误差和重复性
-
 未学习 2.2 TI 高精度实验室 - 温度传感器:灵敏度和增益
未学习 2.2 TI 高精度实验室 - 温度传感器:灵敏度和增益
-
 未学习 2.3 TI 高精度实验室 - 温度传感器:绝对最大和推荐工作点
未学习 2.3 TI 高精度实验室 - 温度传感器:绝对最大和推荐工作点
-
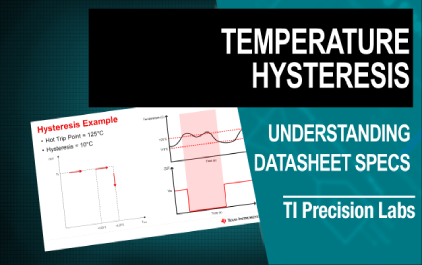 未学习 2.4 TI 高精度实验室 - 温度传感器:温度迟滞
未学习 2.4 TI 高精度实验室 - 温度传感器:温度迟滞
-
 未学习 2.5 TI 高精度实验室 - 温度传感器:比例式
未学习 2.5 TI 高精度实验室 - 温度传感器:比例式
-
 未学习 3.1 TI 高精度实验室 - 温度传感器:校准与补偿
未学习 3.1 TI 高精度实验室 - 温度传感器:校准与补偿
-
 未学习 3.2 TI 高精度实验室 - 温度传感器:非线性和线性化
未学习 3.2 TI 高精度实验室 - 温度传感器:非线性和线性化
-
 未学习 3.3 TI 高精度实验室 - 温度传感器:互换性
未学习 3.3 TI 高精度实验室 - 温度传感器:互换性
-
 未学习 4.1 TI 高精度实验室 - 温度传感器:如何监控电路板温度
未学习 4.1 TI 高精度实验室 - 温度传感器:如何监控电路板温度
-
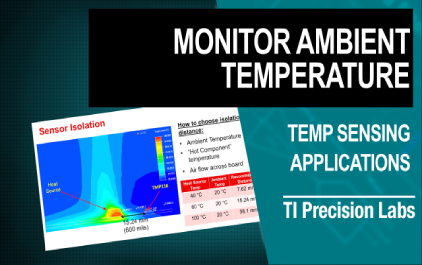 未学习 4.2 TI 高精度实验室 - 温度传感器:如何监控环境温度
未学习 4.2 TI 高精度实验室 - 温度传感器:如何监控环境温度
-
 未学习 4.3 TI 高精度实验室 - 温度传感器:如何监测体温
未学习 4.3 TI 高精度实验室 - 温度传感器:如何监测体温
-
 未学习 一般温度传感器挑战:精度设计
未学习 一般温度传感器挑战:精度设计
-
 未学习 热敏电阻简介
未学习 热敏电阻简介
-
 未学习 优化热敏电阻设计
未学习 优化热敏电阻设计
-
 未学习 热敏电阻软件设计
未学习 热敏电阻软件设计
-
 未学习 使用硅基温度传感器进行热保护
未学习 使用硅基温度传感器进行热保护